Quaternion Math Tutorial

2014-01-23

This tutorial is about quaternions - a way of representing rotations in three-dimensional space. You should be familiar with Vector Math before reading.

Rotations

There are a number of different ways of expressing rotations in 3D space: Quaternions, Euler angles, 3x3 matrices, axis/angles, etc. They all have their own advantages and disadvantages. Euler angles suffer from a problem called gimbal lock, which can make certain rotations impossible. Matrices require more storage space in memory, and are less efficient for vector multiplication. Axis/angles work similarly to quaternions, but are less convenient for interpolation and vector multiplication than quaternions are. Quaternions and matrices tend to be the most convenient options in my experience. To learn more about matrices, I suggest you read Matrix Math.

Euler angles and gimbal lock

Euler angles consist of three rotation angles - one for each axis. The reason that they can be problematic is that these rotations are applied one after another, in a specific order (typically X, Y, Z), each one relative to the last. This makes some rotations impossible. Gimbal lock occurs when the second axis (Y, in this case) is rotated by 90° or -90°. When this happens, the third axis (Z) points in a parallel direction to what the first one (X) was prior to the second rotation (Y), in essence overriding the first rotation and losing one axis of freedom.

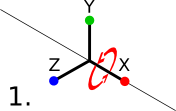
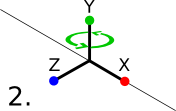
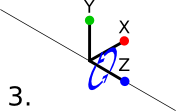
Gimbal lock isn't a problem with quaternions, because they perform their rotation on all axes at once, rather than one at a time.

Axis/angles

Before we continue, it's necessary that I talk about axis/angles briefly. An axis is a direction vector around which to rotate. The angle is the amount of rotation, typically expressed in radians, around that axis. In a right-handed coordinate system, a positive value for the angle rotates counter-clockwise around the axis. If you point the thumb of your right hand in the direction of the axis, a positive rotation angle rotates in the direction that your fingers curl, and a negative angle rotates the opposite direction. The code in this tutorial assumes a right-handed coordinate system.

Definition

A quaternion is a 4-dimensional complex number commonly used to represent a rotation in 3-dimensional space. In this tutorial, I'll be using the following struct for quaternions:

typedef struct Quaternion {
	float x;
	float y;
	float z;
	float w;
} Quaternion;

A quaternion is somewhat similar to an axis/angle. You can think of the x, y, and z components as the axis, and the w component as the angle. Internally, quaternions work very differently from axis/angles; this is simply a convenient analogy. Quaternion internals are complex and very difficult to understand, and will not be discussed in this tutorial. Fortunately, understanding exactly how quaternions do their magic is not a prerequisite to using them. All you need to know is what they can do, how to use them, and how you can implement them in your code.

Usage

A quaternion represents a rotational transformation. What this means is that a quaternion is a "recipe" for a rotation, so to speak. When applied to a vector, the vector is rotated on the axis of the quaternion, by the amount specified in the angle. The "neutral" quaternion that does no rotation at all is known as the identity quaternion. The value of the identity quaternion is {0, 0, 0, 1}.

A quaternion can be converted to and from an axis/angle without any loss of information. A quaternion can be converted to a rotation matrix, but a matrix cannot necessarily be converted back to a quaternion - this is only possible for certain matrices. The following sample code demonstrates these conversions. Note that this code uses the Vector3f struct and the Vector3f_normalize function from Vector Math.

Quaternion Quaternion_fromAxisAngle(Vector3f axis, float radians) {
	Quaternion quaternion;
	float sinAngle;
	
	radians *= 0.5f;
	Vector3f_normalize(&axis);
	sinAngle = sin(radians);
	quaternion.x = axis.x * sinAngle;
	quaternion.y = axis.y * sinAngle;
	quaternion.z = axis.z * sinAngle;
	quaternion.w = cos(radians);
	
	return quaternion;
}

void Quaternion_toAxisAngle(Quaternion quaternion, Vector3f * outAxis, float * outRadians) {
	float sinAngle;
	
	Quaternion_normalize(&quaternion);
	sinAngle = sqrtf(1.0f - quaternion.w * quaternion.w);
	if (fabsf(sinAngle) < 0.0005f) {
		sinAngle = 1.0f;
	}
	
	if (outAxis != NULL) {
		outAxis->x = quaternion.x / sinAngle;
		outAxis->y = quaternion.y / sinAngle;
		outAxis->z = quaternion.z / sinAngle;
	}
	
	if (outRadians != NULL) {
		*outRadians = acos(quaternion.w) * 2.0f;
	}
}

Matrix Quaternion_toMatrix(Quaternion quaternion) {
	Matrix matrix;
	
	matrix.m[0]  = 1.0f - 2.0f * (quaternion.y * quaternion.y + quaternion.z * quaternion.z);
	matrix.m[1]  =        2.0f * (quaternion.x * quaternion.y + quaternion.z * quaternion.w);
	matrix.m[2]  =        2.0f * (quaternion.x * quaternion.z - quaternion.y * quaternion.w);
	matrix.m[3]  = 0.0f;
	matrix.m[4]  =        2.0f * (quaternion.x * quaternion.y - quaternion.z * quaternion.w);
	matrix.m[5]  = 1.0f - 2.0f * (quaternion.x * quaternion.x + quaternion.z * quaternion.z);
	matrix.m[6]  =        2.0f * (quaternion.y * quaternion.z + quaternion.x * quaternion.w);
	matrix.m[7]  = 0.0f;
	matrix.m[8]  =        2.0f * (quaternion.x * quaternion.z + quaternion.y * quaternion.w);
	matrix.m[9]  =        2.0f * (quaternion.y * quaternion.z - quaternion.x * quaternion.w);
	matrix.m[10] = 1.0f - 2.0f * (quaternion.x * quaternion.x + quaternion.y * quaternion.y);
	matrix.m[11] = 0.0f;
	matrix.m[12] = 0.0f;
	matrix.m[13] = 0.0f;
	matrix.m[14] = 0.0f;
	matrix.m[15] = 1.0f;
	
	return matrix;
}

If this looks like a bunch of gibberish, don't worry - as I said before, you don't need to understand the internals of quaternions in order to use them. Quaternion_fromAxisAngle takes an axis vector (normalized) and an angle (in radians), and returns a quaternion representing that rotation. Quaternion_toAxisAngle does the inverse. Quaternion_toMatrix fills a 4x4 matrix with the appropriate values to do the same transformation.

You can multiply two quaternions together as shown in the following code. The effect of this is to concatenate the two rotations together into a single quaternion. Quaternion multiplication is not commutative - the transformation of lhs is applied before rhs, so to speak. I'm also including a convenience function you can use to rotate a quaternion by an axis/angle, as well as convenience functions for performing these transformations inline. Note that this code uses the Vector3f_cross and Vector3f_dot functions from Vector Math.

void Quaternion_multiply(Quaternion * lhs, Quaternion rhs) {
	Quaternion result;
	
	result.x = lhs->w * rhs.x + lhs->x * rhs.w + lhs->y * rhs.z - lhs->z * rhs.y;
	result.y = lhs->w * rhs.y - lhs->x * rhs.z + lhs->y * rhs.w + lhs->z * rhs.x;
	result.z = lhs->w * rhs.z + lhs->x * rhs.y - lhs->y * rhs.x + lhs->z * rhs.w;
	result.w = lhs->w * rhs.w - lhs->x * rhs.x - lhs->y * rhs.y - lhs->z * rhs.z;
	*lhs = result;
}

Quaternion Quaternion_multiplied(Quaternion lhs, Quaternion rhs) {
	Quaternion_multiply(&lhs, rhs);
	return lhs;
}

void Quaternion_rotate(Quaternion * quaternion, Vector3f axis, float radians) {
	Quaternion rotationQuaternion;
	
	rotationQuaternion = Quaternion_fromAxisAngle(axis, radians);
	Quaternion_multiply(quaternion, rotationQuaternion);
}

Quaternion Quaternion_rotated(Quaternion quaternion, Vector3f axis, float radians) {
	Quaternion_rotate(&quaternion, axis, radians);
	return quaternion;
}

Quaternion normalization works the same way as vector normalization, with an extra dimension:

void Quaternion_normalize(Quaternion * quaternion) {
	float magnitude;
	
	magnitude = sqrtf(quaternion->x * quaternion->x +
	                  quaternion->y * quaternion->y +
	                  quaternion->z * quaternion->z +
	                  quaternion->w * quaternion->w);
	quaternion->x /= magnitude;
	quaternion->y /= magnitude;
	quaternion->z /= magnitude;
	quaternion->w /= magnitude;
}

Quaternion Quaternion_normalized(Quaternion quaternion) {
	Quaternion_normalize(&quaternion);
	return quaternion;
}

This function returns the inverse of a quaternion: The quaternion that performs the opposite transformation of the quaternion passed into the function.

void Quaternion_invert(Quaternion * quaternion) {
	float length;
	
	length = 1.0f / (quaternion->x * quaternion->x +
	                 quaternion->y * quaternion->y +
	                 quaternion->z * quaternion->z +
	                 quaternion->w * quaternion->w);
	quaternion->x *= -length;
	quaternion->y *= -length;
	quaternion->z *= -length;
	quaternion->w *= length;
}

Quaternion Quaternion_inverted(Quaternion quaternion) {
	Quaternion_invert(&quaternion);
	return quaternion;
}

You can multiply a vector by a quaternion (without having to go to an intermediate matrix representation) as shown in the following code. For those of you who aren't yet fluent in this sort of terminology, "multiplying" a vector by a quaternion essentially means performing the quaternion's rotation on the vector.

Vector3f Quaternion_multiplyVector3f(Quaternion quaternion, Vector3f vector) {
	Quaternion vectorQuaternion, inverseQuaternion, result;
	
	vectorQuaternion = QUATERNION(vector.x, vector.y, vector.z, 0.0f);
	inverseQuaternion = Quaternion_inverted(quaternion);
	result = Quaternion_multiplied(vectorQuaternion, inverseQuaternion);
	result = Quaternion_multiplied(quaternion, result);
	return VECTOR3f(result.x, result.y, result.z);
}

And finally, there's SLERP. SLERP stands for spherical linear interpolation. As the name suggests, it allows you to interpolate between two quaternions. The value parameter specifies the point of interpolation: 0 for start, 1 for end, 0.5 for the midpoint between start and end, etc. So, if start is a quaternion that rotates 90° on the X axis, end is a quaternion that rotates 180° on the X axis, and value is 0.5, then the function will return a quaternion that rotates 135° on the X axis.

#define SLERP_TO_LERP_SWITCH_THRESHOLD 0.01f

Quaternion Quaternion_slerp(Quaternion left, Quaternion right, float value) {
	float leftWeight, rightWeight, difference;
	Quaternion result;
	
	difference = left.x * right.x + left.y * right.y + left.z * right.z + left.w * right.w;
	if (1.0f - fabs(difference) > SLERP_TO_LERP_SWITCH_THRESHOLD) {
		float theta, oneOverSinTheta;
		
		theta = acos(fabs(difference));
		oneOverSinTheta = 1.0f / sin(theta);
		leftWeight = sin(theta * (1.0f - value)) * oneOverSinTheta;
		rightWeight = sin(theta * value) * oneOverSinTheta;
		if (difference < 0.0f) {
			leftWeight = -leftWeight;
		}
	} else {
		leftWeight = 1.0f - value;
		rightWeight = value;
	}
	result.x = left.x * leftWeight + right.x * rightWeight;
	result.y = left.y * leftWeight + right.y * rightWeight;
	result.z = left.z * leftWeight + right.z * rightWeight;
	result.w = left.w * leftWeight + right.w * rightWeight;
	Quaternion_normalize(&result);
	
	return result;
}

Those are the basics in a nutshell. There are some advanced topics I didn't cover, such as interpolation between more than two quaternions at once, but the basics go a long way. Also, be sure to check out the Quaternion playground companion application at the bottom of this page.

Implementation

Companion application:
Quaternion playground (Mac OS X binary)
Quaternion playground (Win32 binary)
Quaternion playground (source code)